The goal of this assignment was to design a single-pass, Tube and Shell type heat exchanger that produces steam at specified properties needed to drive a 50 MW turbine. To complete the design, we must determine the flow rates of the cycles, the number and lengths of tubes needed, the overall dimensions of the heat exchanger, and the overall heat transfer coefficient.
Determining Pressure Flow Rates
To find the flow rate of steam, we started by assuming the inlet pressure and temperature of water were 60 bar, and 320 degrees celsius respectively. We looked through the thermodynamic superheated tables and found the correlating h to be 2952.6 kJ/kg. We then looked in the saturated table, at a pressure of 1 atm and found that the temperature was 99.63 degrees celsius and had an h of 2258 kJ/kg. We then used the equation W=m(hi-he). We used our turbine power of 50MW as the work and our h values that were found through tables and solved for m (mass flow rate of steam). We found this to be 72 kg/s.
Using the mass flow rate of steam, we solved for total heat transfer rate of the system using Q=mcpT. The average specific heat of steam (cp) was taken as 3.0915. This gave us a Q of 49,052. This heat transfer equation was then used again, with the specific heat of dowtherm A (2.1705), the change in temperature of the dowtherm (350-100=250 degrees celsius), and the same total heat rate (49,052). This produced the mass flow rate of dowtherm to be 90.4 kg/s.
Using the mass flow rate of steam, we solved for total heat transfer rate of the system using Q=mcpT. The average specific heat of steam (cp) was taken as 3.0915. This gave us a Q of 49,052. This heat transfer equation was then used again, with the specific heat of dowtherm A (2.1705), the change in temperature of the dowtherm (350-100=250 degrees celsius), and the same total heat rate (49,052). This produced the mass flow rate of dowtherm to be 90.4 kg/s.
Overall Design Configuration
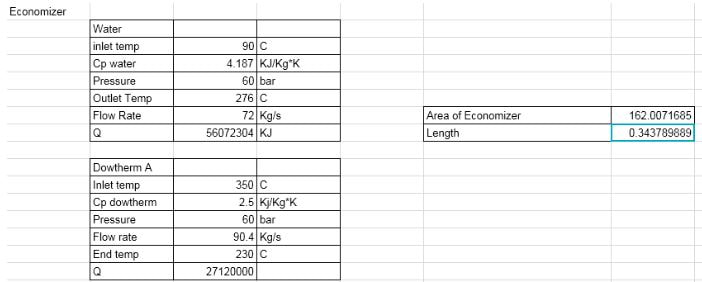
Economizer:
In order to determine a length for the economizer section of the heat exchanger, the initial values of water and Dowtherm A that had been assumed were used. Knowing temperatures and pressures, the Q value for Dowtherm was calculated using the specific heat equation. Once this Q was found, the surface area needed was calculated using the equation A=Q/(U(delta)Twater). The value of U was assumed to be 900. In following sections, it was assumed to be 1200. Using basic thermodynamic principles, it can be assumed that the heat needed to raise the temperature of water came from the other fluid, so the heat of Dowtherm, applied to the temperature increase of water resulted in an area needed over which the required amount of heat would change the temperature of water. The final temperature of water found was the boiling point of water at a pressure of 60 bar.
In order to determine a length for the economizer section of the heat exchanger, the initial values of water and Dowtherm A that had been assumed were used. Knowing temperatures and pressures, the Q value for Dowtherm was calculated using the specific heat equation. Once this Q was found, the surface area needed was calculated using the equation A=Q/(U(delta)Twater). The value of U was assumed to be 900. In following sections, it was assumed to be 1200. Using basic thermodynamic principles, it can be assumed that the heat needed to raise the temperature of water came from the other fluid, so the heat of Dowtherm, applied to the temperature increase of water resulted in an area needed over which the required amount of heat would change the temperature of water. The final temperature of water found was the boiling point of water at a pressure of 60 bar.
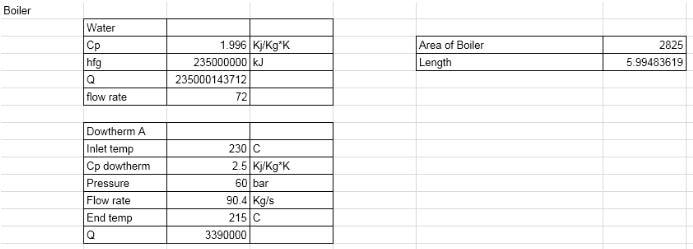
Boiler:
In order to determine the length of the economizer, we followed the same steps as the economizer, but with different values. These different values neglected delta T, because of the insignificant change in temperature in the boiler along with an assumed U of 1200. Therefore, the equation used for area was A=Q/U. This gave us a length of 5.995 m given an assumption of 2500 pipes.
In order to determine the length of the economizer, we followed the same steps as the economizer, but with different values. These different values neglected delta T, because of the insignificant change in temperature in the boiler along with an assumed U of 1200. Therefore, the equation used for area was A=Q/U. This gave us a length of 5.995 m given an assumption of 2500 pipes.
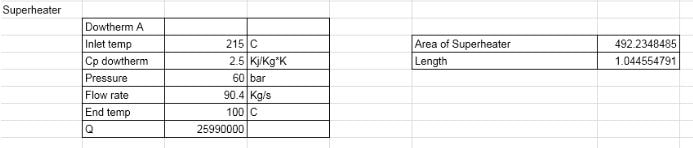
Superheater:
To solve for the length of the superheater, we also used the same equations as we did for the first section. For the superheater we used our assigned end temperature of the boiler, 320 C, along with our known temperature of 100 C that is the Dowtherm leaving our heat exchanger. For the superheater, we also assumed a U of 1200. This gave us a length of 1.045 m.
To solve for the length of the superheater, we also used the same equations as we did for the first section. For the superheater we used our assigned end temperature of the boiler, 320 C, along with our known temperature of 100 C that is the Dowtherm leaving our heat exchanger. For the superheater, we also assumed a U of 1200. This gave us a length of 1.045 m.
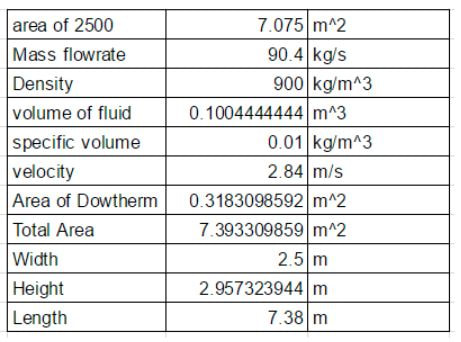
Total Dimensions:
The total length of our heat exchanger was found from adding our three section lengths that we found together. After doing this, we found that our heat exchanger was 7.39 m long. The volume 2500 0.03m pipes was calculated. Knowing the flow rate and specific volume of Dowtherm A, the area of the heat exchanger could be calculated by knowing the area of Dowtherm and adding that value to the area that 2500 pipes would take up.
The total length of our heat exchanger was found from adding our three section lengths that we found together. After doing this, we found that our heat exchanger was 7.39 m long. The volume 2500 0.03m pipes was calculated. Knowing the flow rate and specific volume of Dowtherm A, the area of the heat exchanger could be calculated by knowing the area of Dowtherm and adding that value to the area that 2500 pipes would take up.